lnx的定义域

lnx的定义域是x∈(0，+∞)12。自然对数是以常数e为底数的对数，记作lnN（N>0）。依据可导必连续的特性，lnx在(0，+∞)上到处连续、可导，其导数为1/x>0，所以在（0，+∞）单调增加。又根据反常积分分别发散得知，函数的定义域为（0，+∞），以e为底，值域为R1。

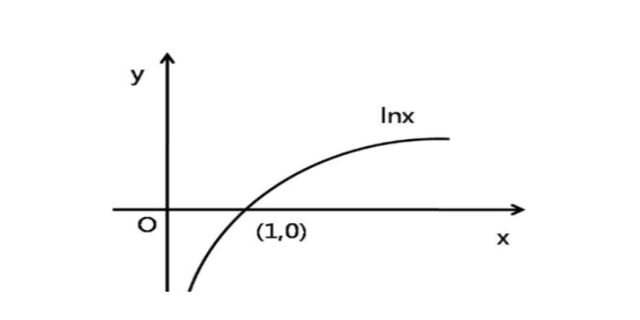
lnx的定义域

自然对数是以常数e为底数的对数，记作lnN（N>0）。在物理学，生物学等自然科学中有重要的意义，一般表示方法为lnx。数学中也常见以logx表示自然对数。

自然对数的定义域是全体正实数。因为自然对数函数的底数e大于0，所以在定义域内，函数是增函数。对于所有x>0，有lnx>0。此外，对于所有x>1，有lnx>1。

在自然对数函数中，自变量x必须大于0。这是因为自然对数的底数是e，而e是一个大于1的数，所以当x小于或等于0时，lnx的值不存在。也就是说，自然对数函数只在正实数范围内定义。